catatan kuliah ke 4
TUGAS
PENGOLAHAN DAN INTERPRETASI DATA CITRA
“CATATAN KULIAH 4”
BERTI S RIMBAEL
NIM 2014-64-007
PROGRAM STUDI ILMU KELAUTAN
JURUSAN MANAJEMEN SUMBER DAYA PERAIRAN
FAKULTAS PERIKANAN DAN ILMU KELAUTAN
UNIVERSITAS PATTIMURA
AMBON
2017
MATERI KULIAH KE 4
BAB 4 STATISTIK DAN ALJABAR CITRA UNTUK VISUALISASI DAN ANALISIS DATA PENGINDERAAN JAUH
Bab ini memberikan pengantar tentang beberapa aspek statistik yang digunakan dalam analisis dan visualisasi citra digital. Sebagai pengantar, tentu saja tidak semua hal yang bersifat teoritis mengenai statistik dipaparkan dalam pembahasan kali ini.
4.1 STATISTIK CITRA
Citra seperti yang sudah dijelaskan pada bab-bab sebelumnya, merupakan sekumpulan piksel dengan nilai tertentu yang mewakili besarnya pantulan atau pancaran spektral objek yang terekam oleh sensor. Dengan demikian, suatu berkas citra tidaklah tersusun atas sekumpulan piksel yang benar-benar homogen, melainkan terdiri dari suatu populasi piksel yang meakili kenyataan di lapangan yaitu beragam jenis penutup lahan dengan beragam karakteristik yang terwakili oleh nilainya.
Seorang analisis citra biasanya melakukan observasi dan evaluasi awal suatu data digital penginderaan jauh melalui beberapa aktivitas berikut (Jensen,2005) :
1. Mengamati frekuensi kemunculan nilai-nilai kecerahan (brightness value,BV) secara individual suatu citra dalam bentuk histogram
2. Mengamati nilai BV piksel secara individual pada layar monitor komputer pada suatu lokasi tertentu atau didalam suatu area geografis
3. Melakukan komputasi mendasar dalam hal statistik deskriptif inivariat piksel-pikselnya, untuk menentukan apakah ada anomali atau penyimpangan yang tidak lazim dalam data citra tersebut
4. Melakukan komputasi statistik multivariat untuk menentukan besarnya korelasi antarsaluran (misalnya untuk melihat adanya redundansi data)
4.1.1 Notasi Matematis untuk Statistik Pengolahan Citra
Notasi berikut ini sering kali digunakan dalam analisis citra.
i = suatu baris dalam citra
j = suatu kolom (atau sampel) dalam citra
k = suatu saluran spektral pada citra
l = saluran spektral yang lain pada citra
n = jumlah total piksel dalam suatu citra
BVjk = nilai kecerahan (brightness value) piksel pada baris kolom j, saluran k
BVik = nilai kecerahan piksel ke-i pada saluran k
BVil = nilai kecerahan piksel ke-l pada saluran k
Mink= nilai kecerahan minimum pada saluran k
Maxk= nilai kecerahan maximum pada saluran k
Rangek= julat nilai kecerahan aktual pada saluran k
quantk = kuantitasi atau tingkat bit-coding untuk saluran k (misalnya 28 = 0-255)
µk = nilai rerata piksel pada saluran k
vark = variansi nilai piksel pada saluran k
sk simpangan baku nilai piksel saluran k
skewnessk = kemencengan distribusi nilai piksel pada saluran k
kurtosisk = kurtosis nilai piksel pada saluran k
covkl = kovariansi antar nilai-nilai piksel pada dua saluran k dan l
rkl = korelasi antar nilai-nilai piksel pada dua saluran k dan l
Xc = vektor pengukuran untuk kelas c yang tersusun atas nilai kecerahan BV ijk dari baris i, kolom j dan saluran k
Mc = rerata vektor untuk kelas c
Mcd = rerata vektor untuk kelas d
µck = nilai rerata untuk data pada kelas c, saluran k
Sck = simpangan baku data pada kelas c untuk saluran k
Vckl = matriks kovariansi kelas c untuk saluran k hingga l, yang ditunjukan sebagai Vc
Vdkl = matriks kovariansi kelas d imtuk saluran k hingga l, yang ditunjukan sebgai Vd
4.1.2 Tendensi Sentral: Rerata, Kemencengan, dan Simpangan Baku
Sama halnya dengan statistik populasi yang lain, tendensi sentral suatu citra menggambarkan pola distribusi nilai kecerahan piksel (BV) dalam citra tersebut. Rumus-rumus berikut ini memberikan gambaran bagaimana suatu cityra yang merupakan kumpulan piksel dengan berbagai nilai mempunyai pola statisti tertentu. Tendensi sentral suatu citra menunjukan kecenderungan distribusi nilai-nilai yang ada dalam suatu citra yang bisa ditunjukan dala bentuk histogram.
Nilai rerata (mean) µk = (4.1)
Nilai rerata citra suatu saluran yang rendah akan ditunjukan oleh tampilan citra (asli) yang relatif gelap. Kalau pun terdapat kenampakan kontras didalamnya, secara keseluruhan akan diperoleh kesan bahwa citra tersebut berona relatif gelap. Sebaliknya, nilai rerata citra suatu saluran yang lebih tinggi diwakili oleh kenampakan citra yang relatif cerah, baik terlihat kontras maupun tidak. Selain nilai rerata µk, ada ukuran tendensi sentral yang lain, yaitu median,modus, simpangan baku, dan kemencengan. Rumus-rumus untuk masing-masing parameter adalah sebagai berikut.
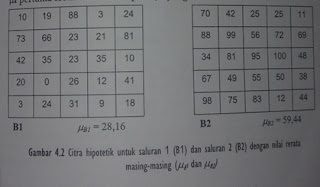
Dua citra hipotetik (Gambar 4.2) dan dua citra sebenarnya (Gambar 4.3) berikut ini mempunyai nilai rerata µk yang berbeda, dimana µk pertama lebih rendah dari pada µk yang kedua.
4.1.3 Variansi, Kovariansi, dan Korelasi
Variansi atau ragam (vark) merupakan salah satu tolak ukjr keberagaman nilai suatu himpunan data. Dalam hal ini, citra merupakan suatu himpunan data nilai piksel sehingga nilai variansi suatu saluran citra merupakan gambaran tentang keberagaman nilai piksel yang ada pada citra tersebut. Variansi merupakan nilai kuadrat dari simpangan baku sehingga dapat dirumuskan sebagi berikut :
Sebenarnya, baik simpangan baku maupun variansi merupakan parameter sebaran data (data spread). Keuntungan penggunaan simpangan baku Sk ialah bahwa parameter ini dinyatakan dalam satuan pengukuran yang sama dengan data pengamatan asli; sementara variansi dinyatakan dalam satuan kuadratnya (Stein,1999).
Apabila tidak ada hubungan antara satu nilai piksel pada suatu saluran dengan nilai piksel yang sama pda saluran lain mka kedua nilai tersebut saling independen, dalam arti bahwa perubahan nilai piksel pada suatu saluran tidak diikuti dengan perubahan nilai piksel yang dapat diprediksi pada saluran lain. Karena pengukuran nilai-nilai spektral piksel tidak dapat independen maka suatu ukuran untuk interaksi antarsaluran itu diperlukan, yaitu dalam bentuk kovariansi,
Kovariansi antara dua saluran k dan l (covkl) dapat dinyatakan dengan rumus berikut ini (Jensen,2005)
Dimana covkl adalah nilai kovariansi antara kedua saluran k dan l, sedangkan Sk dan Sl berturut-turut adalah nilai simpangan baku piksel-piksel di saluran k dan l.
Tabel matriks variansi-kovariansi secara sederhana meberikan gambaran bahwa sepasang saluran yang masing-masing mempunyai nilai variansi tinggi akan cenderung mempunyai nilai kovariansi tinggi pula. Sebaliknya, sepasang saluran yang masing-masing mempunyai nilai variansi rendah akan menunjukan nilai kovariansi antarsaluran yang rendah pula.
Gambar 4.4 citra landsat ETM+ wilayah Maros, Sulawesi Selatan, dimana urutan saluran-saluran
a (biru), b (hijau), c (merah), d (Inframerah dekat), e (Inframerah tengah), dan f (inframerah jauh). Keenam saluran ini yang dijadikan contoh perhitungan variansi-kovariansi pada halaman sebelumnya.
4.2 ALJABAR CITRA
Banyak operasi pengolahan citra bertumpu pada operasi titik (point operation), disamping perhitungan statistik citra dan operasi ketetanggaan (neighbourhood operation). Operasi titik yang dimaksud disini adalah bahwa target operasi pengolahan difokuskan pada nilai piksel (BV) tertentu, dimana pun titik piksel itu berada. Misalkan kita ingin menunjuk pada suatu nilai 20 maka melalui operasi titik sembarang piksel dalam suatu citra dengan nilai 20 akan diperlukan sama.
4.2.1 Prinsip Dasar Aljabar Citra
Liu dan Mason (2009) secara spesifik memandang aljabar peta yang diterapkan pada citra merupakan kelompok operasi titik multipeta ( multi image point operations). Operasi ini berlangsung secara multivariat, di mana jumlah saluran menggantikan jumlah variabel dan dijalankan pada piksel demi piksel secara independen tanpa mempertimbangkan kondisi piksel-piksel yang bertetangga. Secara umum terlihat pada fungsi berikut :
Y = f (X1,X2.X3,.... Xn),
Dimana n adalah jumlah saluran atau lapisan.
Perlu ditekankan disini bahwa operasi aljabar citra (atau peta) sepenuhnya bersifat lokal, berbasis pixel to pixel. Untuk itu dapat diturunkan suatu deskriptor. Xi adalah citra, dimana i= 1,2,3 .... n, yang merepsentasikan baik saluran ke-i maupun sembarang pixel di dalam saluran ke i himpunan data citra X, dimana Xi € X.
4.2.2 Jenis-jenis Operasi Aljabar Citra
1. Penjumlahan Citra
Penjumlahan citra menghasilkan citra baru hasil penjumlahan dengan nilai baru yang diberi bobot. Secara umum hal itu dapat dirumuskan sebagai berikut:
Y = ......................................... (4.8)
Dimana Y adalah citra baru, Wi adalah bobot citra masukan Xi, dan k adalah faktor skala. Jadi, apabila Wi sama dengan 1 untuk i = l,......., n dan k = n, maka rumus diatas menghasilkan citra rerata dari seluruh citra masukan.
Gambar 4.5 atas : penjumlahan citra dengan menggunakan nilai piksel asli memberikan citra baru dengan nilai atau julat melebihi kondisi asli dan bisa menyebabkan penyimpangan dalam tingkat bit yang lebih tinggi. Bawah : masing-masing saluran masukan diberi bobot (dalam hal ini bernilai 1) dan dinagi dengan jumlah saluran masukan (4). Hasilnya merupakan nilai rearata dan masih masuk di dalam julat nilai asli.
Penjumlahan citea bisa diterapkan pada sekumpulan saluran pada citra multispektral (gambar 4.5) mengingat bahwa setiap piksel pada suatu citra saluran i dapat terkontaminasi oleh derau (noise), sementara piksel yang memuat derau tidak muncul pada sembarang posisi yang sama pada saluran-saluran yang berbeda, maka penjumlahan citra dengan efek mereratakan seluruh nilai pada seluruh saluran akan ‘membagi’ derau pada satu piksel dengan jumlah saluran yang ada (Liu dan Mason, 2009).
2. Pengurangan Citra
Seperti halnya penjumlahan citra, pengurangan citra juga memperhatikan jumlah dan bobot citra masukan. Rumusnya adalah sebagai berikut :
Y = (Wi Xi – Wj Xj ) ............................................... (4.9)
Dimana Xi dan Xj berturut-turut adalah citra saluran i dan j; sementawa Wi dan Wj masing-masing adalah bobot dari citra Xi dan Xj.
Liu dan Mason (2009) menegaskan bahwa dalam pengurangan citra, besarnya bobot citra masukan sangatlah penting, sebagai contoh, apabila citra masukan Xi mempunyai kontras yang jauh lebih tinggi daripada Xi maka selisih keduanya dengan menggunakan bobot Wi dan Wj tidak akan menggambarkan selisih yang sebenarnya. Untuk itu, diperlukan suatu pra-pemrosesan yang antara lain menggunakan teknik histogram matching, dimana histogram kedua citra disesuaikan terlebih dahulu untuk menghasilkan pola dan julat yang kurang lebih sama. Apabila beda kontras antara kedua citra Xi dan Xj tidak terlalu besar maka nilai bobot Wi dan Wj = 1 bisa digunakan.
3. Perkalian Citra
Perkalian citra didefeniskan sebagi berikut:
Y = Xi . Xj ................................................. (4.10)
Dimana Y adalah citra baru hasil perkalian, sementara Xi dan Xj berturut-turut adalah citra saluran i dan j. Dalam perkalian ini setiap nilai piksel pada suatu posisi baris dan kolom dalam citra i dikalikan dengan setiap nilai piksel pada posisi baris dan kolom yang sama pada citra j. Perkalian terjadi dengan cara demikian karena meskipun citra pada dasarnya adalah suatu array 2 dimensi, tetapi citra bukanlah matriks sehingga operasi perkaliannya tidak sama dengan operasi perkalian pada matriks.
Gambar 4.6 Perkalian citra tanpa penskalaan kembali hasil perkalian (citra Y, atas) dan dengan penskalaan melalui operasi akar kuadrat (citra Y, bawah )
Syarat lain harus dipenuhi dalam perkalian citra adalah bahwa kedua citra i dan j yang terlibat memiliki referensi spasial yang sama. Dalam paket pengolah citra digital murni, hal ini bisa dipenuhi oleh dua citra i dan j yang mempunyai ukuran piksel yang sama.
Hasil perkalian citra adalah citra baru dengan nilai yang jauh lebih besar dari nilai maksimum pada citra masukan (asli). Kondisi dengan nilai yang jauh lebih besar ini bisa berdampak pada tidak jelasnya gambar yang tersaji pada citra, kecuali melalui mekanisme perentangan kontras yang proporsional. Cara lain adalah dengan menerapkan operasi akar terhadap rumus asli :
Y = ................................................................. (4.11)
4. Pembagian citra
Pembagian citra secara sederhana dapat dirumuskan sebagai berikut.
Y = .............................................................................. (4.12)
Sama halnya dengan rumus-rumus terdahulu terkait dengan aljabar citra, Y menyatakan citra baru hasil komputasi, sementara Xi dan Xj berturut-turut mewakili citra saluran i dan saluran j. Hal penting yang perludiperhatikan disini adalah adanya kemungkinan bahwa penyebut ( piksel pada citra Xj) bernilai 0. Apabila hal ini terjadi maka nilai tak terdefenisikan pada citra keluaran Y akan dihasilkan. Untuk mengatasi masalah semacam ini, kadang kala julat nilai 0-255 pada citra Xj terlebih dahulu digeser menjadi 1-256, meskioun hal ini juga menjadikan masalah bagi sistem yang hanay bisa menyimpan pada julat 0-255. Cara lain adalah melalui pengondisian logis untuk setiap perhitungan yang melibatkan penyebut bernialai 0 agar diberi hasil dengan nilai maksimum.
5. Indeks
Dalam analisis citra digital multispektral, kita akan banyak akan berurusan dalam indeks spektral. Indeks spektral merupakan suatu operasi global pada citra yang melibatkan dua saluran spektral atau lebih dalam bentuk aljabar citra. Indeks-indeks ini dimanfaatkan untuk berbagai keperluan, misalnya untuk penonjolan aspek kerapatan vegetasi, penonjolan aspek tanah dan batuan, dan juga penonjolan aspek kerapatan bangunan kekotaan.
Contoh operasi aljabar sederhana untuk indeks vegetasi adalah Ratio Vegetation index (RVI) dengan rumus :
RVI .......................................................................... (4.13)
Yang pada dasarnya merupakan bentuk nisbah sederhana (simple ratio) contoh lain adalah Normalised Difference Vegetation Index (NDVI) yang sangat populer dalam berbagai kajian vegetasi dan lingkungan yang memerlukan parameter kerapatan vegetasi. Rumus NDVI adalah sebagai berikut.
NDVI = .......................................................................... (4.13)
Model-model indeks lain yang bertumpu pada aljabar citra bisa dibaca pada bab 7.
6. Penggunaan Operator Matematis Lain
Disamping operasi aritmetik, pengolahan citra juga dapat melibatkan operator matematis lain, seperti fungsi algoritma natural (In) dan fungsi-fungsi trigonometrik ( sin,cos,tan,arctan, dan sebagainya). Sama halnya dengan formula terdahulu, penerapan suatu fungsi matematis terhadap citra Xi atau Xj cukup disajikan dengan menuliskan fungsi matematis di depannya, misalnya:
Y = In (Xi) + In (Xj) .................................................. (4.15)
Y = sin (Xi) – cos (Xj) ............................................... (4.16)
7. Standarisasi Saluran Spektral
Ada lagi jenis operasi aljabar citra yang disebut standarisasi. Operasi ini melibatkan beberapa saluran spektral dan biasanya ditujukan untuk menghasilkan saluran-saluran individual dalam himpunan data (dataset) multispektral yang relatif lebih bebas pengaruh/efek bayangan. Secara umum rumus untuk standarisasi saluran-saluran individual adalah sebagi berikut (Liu dan Mason, 2009):
Yi =
Dimana Yi adalah citra baru (saluran baru) saluran yang distandarisasi, Xi adalah citra saluran lama i yang menjadi masukan, dan k adalah jumlah saluran dengan rentang dari 1,2,3...., hingga λ.
Sebagai contoh, kalau kita punya citra multispektral Ikonos dengan 4 saluran spektral (biru/B, hijau/H, merah/M, dan inframerah dekat/IMD), maka setiap nilai kecerahan di setiap saluaran bisa distandarisasi dengan cara :
Dengan cara standarisasi ini variasi spektral antarsaluran, khususnya pada tingkat piksel, dapat dipertajam dengan lebih baik karena menggunakan nilai penyebut yang sama.
4.3 VISUALISASI CITRA
Citra digital sebagai data biner sebenarnya tidak disimpan sebagai ‘citra’ yang sesungguhnya. Telah disebutkan pada bab terdahulu bahwa citra digital, meskipun disimpan dalam berbagai format, tidaklah menggambarkan ruang dalam arti yang sebenarnya. Informasi yang jelas ada dalam data digital ini hanyalah angak dengan kisaran 0-255, kalau data disimpan dalam 8 bit-coding, 0-511 kalau disimpan dalam 9 bit-coding, 0-1023 kalau disimpan dalam 10 bit-coding, dan seterusnya. Bila angka ini, dipandang sebagai representasi nilai respons spektral yang tercatat oleh sensor, maka kita dapat mengatakan bahwa data digital ini tersimpan dalam domain spektral.
4.3.1 Tampilan Monokromatik
Nilai kecerahan atau nilai digital ini kemudian dipresentasikan pada layar monitor dengan mengikuti konvensi bahwa nilai sangat rendah (dalam hal ini 0) disajikan dengan rona sangat gelap atau hitam; sementara nilai sangat tinggi disajikan dengan rona sangat cerah atau putih. Hal ini selaras dengan persepsi mata manusia bahwa sesuatu yang gelap berkorelasi dengan tingkat pantulan yang sedikit (rendah), sedangkan sesuatu yang cerah berkorelasi dengan tingkat pantulan yang banyak (tinggi).
4.3.2 Citra Komposit Warna
1. Teori Kubus Warna
Sejak di sekolah dasar dan menengah, kita diajarkan tentang pengertian bahwa kenampakan warna sebenarnya tersususan atas tiga warna dasar, yaitu biru,hijau, dan merah. Warna-warna lain muncul sebagai kombinasi dari warna-warna dasar tersebut. Pengertian ini didasari oleh teori kubus warna (Gambar 4.7), dimana warna merah, hijau, dan biru diletakan berturut-turut pada sumbu merah,hijau, dan biru. Besarnya nilai di sepanjang masing-masing sumbu mewakili kekuatan sinyal atau intensitas masing-masing warna, yang kalau dikonversi menjadi sistem digital menjadi 0-255, 0-511, 0-1023 dan seterusnya, tergantung pada kepekaan sensor yang digunakan.
Apabila tidak ada warna biru maka kombinasi intensitas warna merah maksimumm dengan intensitas warna hijau maksimum akan menghasilkan warna kuning. Jika warna merah tidak ada maka kombinasi intensitas warna hijau maksimum dengan intensitas warna biru maksimum akan menghasilkan warna cyan. Kalau warna hijau yang tidak ada maka kombinasi intensitas merah maksimum dengan intensitas warna biru maksimum akan menghasilkan warna magenta. Penyusun warna semacam ini disebut penyusun warna aditif, di mana warna-warna primer (biru,hijau, dan merah) menjadi komponen penyusunnya.
Berdasarkan teori kubus warna (RGB colur cube) ini, citra beberapa saluran dapat disajikan pada layar monitor dan kemudian dicetak. Satu himpunan data 9dataset) citra multispektral dapat terdiri atas tiga saluran, yang masing-masing dapat diberi warna biru,hijau dan merah. Namun tidak jarang dijumpai, satu dataset terdiri dari empat,tujuh dan bahkan belasan saluran spektral. Satu dataset citra hiperspektral bisa terdiri dari 220 saluran spektral, dan secara sederhana hanya tiga diantaranya yang dapat dipilih untuk menyusun citra komposit, yaitu citra berwarna yang tersusun atas 3saluran, yang masing-masing diberi wana biru,hijau dan merah.
2. Teori warna IHS (intensity-hue-saturation)
Teori warna dengan kubus RGB tidak dapat menjelaskan seberapa murni dan seberapa jenuh komponen warna larena dalam komponen itu setiap warna diwakili oleh sumbu X, Y dan Z hanya menentukan tingkat intensitas warnanya saja. Untuk mengatasi kelemahan ini, teori lain digunakan, yaitu yang disebut IHS.
Ketiganya merupakan komponen-komponen yang independen intensitas merupakan tingkat dari intensitas kemerahan,kehijauan, dan kebiruan.seperti yang ditunjukan oleh kubus RGB hue adalah komponen warna untuk meneunjukan warna itu sendiri saturationa merupakan ukuran untuk menenjukan seberapa murni/jenuh warnanya, dikaitkan dengan pencampuran oleh warna putih. Semakin pucat warnanya, semakin rendah saturationnya. Semakin rendah intensitasnya, semakin gelap mendekati hitam objeknya. Semakin tinggi intensitasnya hue, maka semakin merah objeknya.
a. Tranformasi IHS berdasarkan RGB
Ada beberapa pandangan dan teori tenteng nilai kuantitatif IHS jika dikaitkan dengan nilai RGB, berikut komponen rumus warna dalam IHS menurut jansen (2005), liu dan mason (2009), dan gao, (2010). Berdasarkan rumus transformasi ini, nilai I, H, dan S suatu citra yang setidaknya tersusun atas 3 saluran RGB sebagai berikut:
I = R + G + B (jensen, 2005)…………………………………………………………...(4.22)
Sementara itu ,liu dan mason merumuskan intensiti sebagai berikut;
I = ( R + G + B ) (liu dan mason, 2009)……………………………………………..(4.23)
Disamping itu, gao (2010) merumuskan dengan sedikit berbeda yaitu;
I = (Gao, 2010)……………………………..…………………………………(4.24)
Sepintas ketiga rumus tersebut membingungkan, miskipun demikian apabila kita lihat kembali keprinsip aljabar citra pada bab ini , maka rumus tersebut adalah selaras. Penggunaan nilai dan merupakan varian dari penjumlahan total R, G, B, yang disertai dengan pertimbangan bahwa penjumlahan total akan menyebabkan nilai baru/yang melampui julat asli citra penyusun pada sistem pengolahan citra yang lebih maju, secara otomatis rumus jansen (2005) kemudian diproses dengan pensklaan kembali dengan menggunakan atau .
Kemudian nilai hue (H) dihitung dengan rumus berikut;
H = (jensen,2005)…………………………………………………………………(4.25)
Atau H = arccos .(liu dan mason, 2009)……………………………………….(4.26)
Dimana; V = + )-(RG+RB+GB)
Atau, H = arccos (Gao, 2010)…………………………………………………(4.27)
Sementra itu, dengan mengacu pada jensen (2005), liu dan maosn (2009), goa (2009) konsekuensi Yang muncul pada rumus saturation adalah sebagai berikut;
I = (jensen , 2005)………………………………………………………….(4.28)
Atau, S= sehinnga,
S= (liu dan mason, 2009)……………………………………………..(4.29)
Atau S= ( Gao, 2010)………………………………………(4.30)
Rumus-rumus di atas tentunya tidak hanya berlaku pada sistem multispektral yang terdiri dari 3 saluran RGB saja, pengertian RGB disi lebih tepat mengacu pada saluran yang diberi warna merah,hujau dan biru. Oleh karena itu, apabila citra masukannya adalah infra merah jauh deberi warna B, maka rumus I, H, S juga dimasukan nilai-nilai pixel. Pada saluran inframerah dekat,tengah dan jauh.
b. Dari RGB ke IHS kembali ke RGB
Sekali citra baru berupa intensity, hue, dan saturation terbentuk maka ketigannya dapat dijadikan masukan dalam penyusunan komposit warna dengan mengembalikannya adalah warana pada citra I, hijau pada H, biru pada S. penyusunan komposisi melalui transformasi RGB-HIS-RG ini kadang kala dapat menghasilkan komposit warna yang bagus dan mudah di interprestasikan, namun kadang kala juga menghasilkan citra yang lebih sulit untuk di mengerti.
3. parameter statistik untuk kualitas citra komposit
Dengan banyaknya kemungkinan untuk dapat menghasilkan citra komposit berdasarkan jenis masukan saluran spektral dan cara representasi warnanya, kemmudian timbul pertanyaan. Adakah suatu parameter yang dapat digunakan untuk menilai suatu citra komposit lebih baik/lebih buruk daripada yang lain? Sebenarnya ukuran semacam ini.kalaupun ada tidak dapat digenerasikan begitu saja, sehingga konsep kejelasannya pada citra juga bersifat relatif tergantung jenis kenampakan yang dianalisis. Diasamping itu, persepsi warna dan pola yang muncul pada citra juga bisa berbeda-beda untuk penafsir yang berbeda di latar belakangnya miskipun demikian, mengacu kembalinya keprinsip dasar stasistik dapat digunaan untuk membantu menemukan kualitas citra komposit, berdasarkan saluran-saluran penyusun, yaitu melaui optimum index faktor (OIF), yang dikembangkan oleh Ccaves et al (1982).
optimum index faktor (OIF)
Ccaves et al (1982) mengembangkan suatu parameter untuk menilai kualitas citra komposit secara statistik. Parameter ini disebut dengan OIF, misalnya terdapat citra dengan n saluran maka nilai OIF ini dihitung untuk sembarang kombinasi 3 saluran sebagai berikut (jensen, 2005).
Dimana Sk adalah simpangan baku iuntuk saluran k, dan abs (n) adalah harga mutlak untuuk koefisien korelasi antara sembarang pasangan 2 saluran dari ke3 saluran tersebut.
Mengacu kembali kedasar sattistik citra maka nilai OIF ditentukan oleh 2 hal utama. Paertam adalah nilai simpangan baku seluruh pixel dalam seluruh citra yang dilibatkan. Kedua adalah besaranya koefisien korelasi antar saluran yang dilibatkan kedalam penyusunan komposit. Semakin beragam nilai pixel dalam suatu saluran, semakain besar pula nilai simpangan bakunya. Apabila 3 saluran masukan semua sangat beragam nilainya.maka nilai pembilang menjadi besar. Disisi lain, apabila 3 saluran yang dilibatkan tersebut tidak saling berkorelasi, maka nilai penyebut akan cenderung kecil dan hal ini akan berpotensi untuk menghasilkan nilai OIF yang besar. Semakin besar nilai OIF, semakin bagus kualitas citra kompositnya secara ststistik. Besarnya koefisien antar saluran tersaji dalam bentuk matriks korelasi pada tabel 4.3 kelima saluran tersebut dapat disusun menjadii citra komposit warna banyak 6 kombinasi, yaitu; B1, B2, B3. B1,B2,B4.B1,B2,B5. B1,B3,B4.B1,B3,B5,B1,B4,B5. Dari rumus OIF, tidak ada perbedaan nilai kualitas citra komposit yang dihasilkan apabila posisi salah satu/ seluruh saluran dipertukarkan dalam pemberian waranya, misal B1 diberi biru/hijau/merah. Besarnya nilai OIF untuk masing-masing kombinasi tersaji di tabel 4.4
Bagian yang diasir abu-abu menunjukan bahwa nilai koefisien korelasinya sama untuk pasangan yang sama, misal B3-B4 dengan B4-B3.
Hasil tersebut menunjukan bahwa pasangan atau kombinasi saluran terbaik untuk komposit warna citra multispektral hipotetik adalah B1, B4, B5 (OIF = 44,90). Diikuti oleh B1, B3, B4 (OIF = 43,91), sedangkan kombinasi yang paling buruk adalah B1, B2,B3 (OIF = 18,37).setiap kombinasi yang paling buruk adalah B1, B2, B3, (OIF = 18,37). Setiap kombinasi ini akan memberikan nilai OIF yang sama miskipun posisi setiap saluran dalam urutan RGB dibolak-balik. Perlu diperhatikan di bawah miskipun statistik perhitungan OIF ini logis dalam menunjukan kombinasi saluran terbaik, dalam kenyataan tiadak selalu demikian. Mengingat bahwa rumus OIF disusun oleh parameter simpangan baku dan koefiseian korelasi antar saluran maka citra yang mengalami gangguan spektral tertentu, seperti banyak bad lines, noise atau berkabut. Akan membentk komposit dengan nilai OIF tertenggi. Oleh karena itu, penilain visual tetap diperhatikan setelah pemeringkatan melalui OIF dilaksanakan. Ada kemungkinan bahwa kombinasi saluran dengan OIF diperingkat 2 atau 3 justru lebih baik.
4.3.3 “Look-Up Table” (LUT)
Telah dijelaskan pada bagian terdahulu bahwa secara default, citra saluran tunggal biasa di tampilkan dalam gradisi keabuan, sementara citra kompaositt selalu disajikan dalam bentuk komposit warna dengan menggunakan kombinasi RGB atau yang lain, misalnya IHS. Miskipun demikian, ada beberapa pertimbangan lain dalam tampilan citra, terutama ketika perbedaan antara tingkat bit-coding citra masukan dengan tingkat bit-coding layar monitor. Di samping ituu, kadang kala efektifitas tampila untuk suatu fenomena bisa meningkat ketika citra tidak disajikan dalam gradasi keabuan, melainkan denagn gradasi warna tertentu.
I. LUT untuk Gradasi Keabuan (Grey Scale)
Hampir semua paket pengelolacitra selalu menggunakan asumsi bahwa masukan citra selalu memiliki 256 tingkat keabuan. Bila nilai kecerahan ini kita sebut BV (brightness value) maka dalam program selalu dinyatakan bahwa BV input berkisar dari 0 sampai 225. Masukan nilai dengan julat
2. LUT Untuk Warna-warna lain
Teknik pseudo colour digunakan untuk menonjolkan perbedaan nilai spektral yang tipis, tanpa melakukan perentangan kontras. Dengan pseudo colour, piksel-piksel bernilai ‘rendah’ diberi warna biru, sedangkan nilai ‘tengah’ diberi warna hijau, dan nilai ‘tinggi’ diberi warna merah. Untuk monitor 8 bit, nilai terendah yaitu nol, diberi warna hitam; warna biru untuk nilai1,2,3,...; warna hijau untuk nilai 128,129,130,...; dan akhirnya warna merah untuk 255. Gradasi semacam ini dapat pula diterapkan dengan memberikan kombinasi warna yang berbeda, misalnya dari biru gelap,ungu,magenta,merah,pink, sampai dengan putih.
Disamping itu masih banyak lagi teknik presentasi presentasi piksel dalam warna yang semuanya lebih mengandalkan perbedaan warna berulang untuk setiap selang nilai tertentu, misalnya setiapa 8 tingkat kecerahan, 16 tingkat kecerahan dan sebagainya. Beberapa paket perangkat lunak untuk pengolahan menyediakan pilihan LUT cukup banyak.
3. LUT untuk citra komposit warna
Dalam penyusun citra komposit warna, setiap saluran masukan pada umumnya mempunyai tingkat bit-coding minimal 8 atau setara dengan julat 0-255. Apabila suatu citra komposit tersusun atas 3 saluran yang masing-masing mempunyai kedalaman informasi piksel 8 bit (28 tingkat kecerahan, atau 256 gradasi keabuan) maka citra komposit yang terbentuk akan mempunyai 28x3= 224 atau setara sekitar 16,77 juta warna.
Teknik lain , yang masih juga merupakan kompresi citra, adalah penyusunan fungsi matematis ketiga saluran untuk menghasilkan citra baru, yaitu citra komposit. Melalui fungsi matematis ini, kemampuan layar yang hanya 8 bit tidak perlu dipaksa untuk berfungsi maksmimal, tetapi si pemrogram atau pengguna dapat mengatur keluaran nilai piksel maksimum yang baru. Sebagai contoh, tiga saluran (1,2, dan 3) yang masing-masing memiliki julat 0-255 akan dipadukan menjadi citra komposit warna. Sebagai langkah awal, setiap saluran dimampatkan menjadi citra baru dengan julat 0-5. Selanjutnya citra komposit warna adalah lekuaran yang dihasilkan oleh formula :
Citra komposit = 36x (saluran_1) + 6x(saluran_2) + saluran_3
Dimana :
Saluran_1 = inframerah dekat
Saluran_2 = m,erah
Saluran_3 = hijau
4.4 SISTEM PENGOLAH CITRA
Saat ini terdapat banyak sekali perangkat lunak pengolah citra yang beredar di pasaran, hal ini berbeda jauh dibandingkan kondisi sebelum 1990-an, dimana sebagian besar sistem pengolah citra digital penginderaan jauh dijalankan pada plattform atau sistem informasi untuk komputer besar, terutama mainframe. Berkembangnya komputer personal (PC) pada dekade 90an dan kemudian laptop pada dekade abad ke 21 telah membuat sistem pengolah citra penginderaan jauh dapat dijangkau oleh siapa saja.
Perangkat lunak yang dikhususkan bagi pengolahan citra penginderaan jauh cukup banyak di pasaran, ENVI (Environment for Visualising Image,( Gambar 4.10) adalah salah satu jenis perangkat lunak yang paling populer saat buku ditulis, dengan kelengkapan fungsi analisis yang sangat baik untuk ukuran sistem berbasis Microsoft Windows. ENVI diproduksi oleh RSI (Research Systems Institute) Inc. di Amerika Serikat dan disajikan secara terintegrasi dengan modul pemrograman IDL (Interractive Data Languange). Perangkat lunak ini mempunyai kemampuan yang bagus dalam mengelola data berukuran cukup besar, baik dalam hal dimensi (ukuran baris-kolom) citra maupun dalam hal jauh saluran (hingga hiperspektral)
Gambar 4.10 Tampilan perangkat lunak ENVI
Fasilitas dasar ENVI yang menonjol adalah kemampuan membaca dan mengonversi data (impor ekspor) penginderaan jauh dalam berbagai format, melakukan pemotongan citra (membuat subimage) baik dalam hal ukuran baris-kolom maupun jumlah saluran dalam berbagai ukuran acuan (peta,citra, maupun pilihan baris-kolom secara bebas), fasilitas lain adalah kemampuan melakukan koreksi dan kalibrasi citra, baik secara geometrik maupun radiometrik. Kelengkapan koreksi dan kalibrasi radiometrik termasuk unggul dibandingkan perangkat lunak lain.
Kemampuan pengolah citra yang terbatas dimiliki oleh perangkat lunak SIG berbasis vektor, seperti MapInfo dan ArcView serta ArcGIS. Pada perangkat-perangkat lunak ini fasilitas pengolahan hanya tampilan (display) citra komposit dari sejumlah pilihan saluran spektral (tidak hanya tiga) dengan fasilitas dengan fasilitas penajaman; kecuali ArcGIS yang menyajikan fasilitas klasifikasi multispektral sederhana.
Modul-modul SIG yang disediakan pada umumnya berbasis model data raster. Hal ini sangat wajar karena pada dasarnya logika analisis spasial peta raster dan citra digital hampir sama, dimana citra multispektral dipandang sebagai data multivariat. Perangkat-perangkat lunak ini misalnya adalah ERDAS Imagine, Idrisi, dan ILWIS.
ERDAS (Earth Resource Data Analysis System, Gambar 4.11) Imagine dapat disebut sebagai perangkat lunak dengan fasilitas pengolah citra yang sangat lengkap dan SIG berbasis raster yang juga lebih dari memadai.
Setiap proses pengolahan dengan Imagine memberikan opsi pada pengguna/analisis, apakah akan menyimpan data dengan format tertentu, yang kadang kala tidak disajikan secara jelas pada perangkat lunak lain. Sebagai contoh, hasil proses suatu penajaman atau pemfilteran, apakah akan disimpan sebagai unsigned 8 bit (0-255), atau integer, atau data riel (floating nilai pecahan). Proses pengolahan yang dipandu dengan dialog box sangat membantu dan membimbing pengguna atau analis dalam mengambil keputusan dan mempelajari proses berpikir analisis citra dalam oerangkat lunak tersebut.
Meskipun fasilitas analisis spasial (SIG) dalam Imagine cukup baik,ada satu hal yang dengan cermat perlu dipegang oleh pengguna atau analisis, yaitu bahwa setiap label diwakili dengan angka (nilai piksel), yang pada dasarnya memang merupakan model tipikal SIG berbasis raster. Di samping itu, kurangnya fasilitas konversi data vektor ke raster dan model-model statistik spasial pendukung juga merupakan catatan penting. Lepas dari itu, kemampuan analisis spasial melalui konteks atau ketetangaan merupakan keunggulan Imagine dibandingkan kebanyakan perangkat lunak pengolah citra dan SIG terintegrasi lainnya.
Disaijkan oleh ENVI, lengkap dengan menu-menu post-classification processing yang tidak terkait dengan fungsi-fungsi SIG. visualisasi dan anilisi data topografi juga disediakan, dilengkapi dengan modul analisis radar.
ENVI menawarkan fleksibilitas dalam pengolahan citra melalui IDL, dimana pengguna dapat memprogram sendiri modul yang diinginkan, kemudian diintegrasikan dengan menu yang ada. Model-model dan formula anilis citra dapat dikembangkan dengan pemprogramkan melalui IDL. Kekurangan utama ENVI adalah kemampuan untuk mengintegrasikan analisis citra spektral deangan data spasial yang lain . di samping itu fasilitas presentasi kartografis hasil analisis citra khususnya hasil klasifikasi masih sangat terbatas.
Perangkat lunak dengan fungsi yang hampir serupa dengan ENVI adalah ER-Mapper yang pada awalnya dikembangkan di australia. ER-Mapper menawarkan fleksibilitas dalam visualisasi yang dapat dilakukan melaui langkah-langkah yang bervariasi. Kemampuannya untuk koreksi geometri dan penyusunan mosaik citra secara digital termasuk unggul. Fitur utama paling menonjol pada perangkat lunak ini adalah kecepatan pemprosesan dan tampilan yang disertai dengan penyimpanan berkas yang sangat efisien, yaitu melalui penyimpanan defenisi penurunan data yang disebut algoritma. Berkas algoritma hanya menyimpan defenisi dari proses yang dilakukan dan disimpan dalam bentuk tesk. Ketika berkas algoritma di aktifkan, proses pun dijalankan pleh program dengan kecepatan yang tinggi.
ER-Mapper menawarkan modul-modul seperti yang dierikan oleh ENVI keunggulannya dibandingkan ENVI adalah kemampuan untuk menerapkan klasifikasi citra melalui feature space dan bukan melalui image space, sperti ini biasanya dilakukan dengan perangkat lunak lain. Dengan demikian, kelas dapat dipilih berdasarkan pengetahuan atas posisi objek dalam ruang spektral multi dimensional. Miskipun demikian sebagai perangkat lunak pengolah citra ER-Mepper juga mempunyai kelemahan dalam penyajian karto-grafis hasil klasifikasi maupun citra komposinya. Disamping itu, kemampuan untuk bekerja dengan data spasial bukan pengindraan jauhpun sangat terbatas.
Agak bersembarang dengan ERDAS image, ILWIS (gambar 4.12) menawarkan modul SIG berbasis raster yang lebih lengkap, dengan fasilitas pengolah citra yang relatif lebih sedikit. Miskipun kemmampuan pengolah citranya lebih ungul dibandingkan kebanyakan SIG manapun juga. ILWIS pada awalnya dikembangkan di ITC, negeri belanda, berdasarkan proyek penglahan DAS disumatra selatan dan di amerika selatan. Saat ini ILWIS sudah beralih kedomain open source dan dapat di download secara gratis di www.52north,org.
ILWIS menunjukan kemampuan menginegrasikan pengolahan citra dan SIG raster melalui fasilitas kalkulator peta. Melalui toolbox approach, ILWIS tidak membedakan peta dan citra secara bersebrangan, kecuali dalam properties yang menyatakan domain datanya. Operasi dalam kalkulasi peta berbasis pada kombinasi aljabar peta/citra, pengondisian logis dan pergaitan atribut dengan nilai pixel atupun poligon. Dalam pengolahn citra, keterbatasan ILWIS terutama dalam menu-jadi untuk pra-pemprosesan yang tidak terlalu lengkap,miskipun hal ini bisa, dilakukan dengan bantuan kalkulator peta. Begitu juga fasilitas uji akurasi serta analisis citra lanjut seperti untuk data hiperspektral dan radar.
Kemampuan ILWIS yang paling menarik adalah dalam mengintegrasikan data vektor, data raster, dan data citra digital. ILWIS mempunyai menu untuk masukan data vektor melalui fasilitas digitasasi-baik dengan meja digiser. Maupun on-screnn, menyusun topologi hingga menjadi data vektor tingkat tinggi. Perangkat lunak ini juga mempu melakukan analisis geostatistik dari data vektor titik/garis kadata raster kontiniu, untuk diintegrasikan dengan citra. ILWIS sangat bermamfaat untuk post-classification processing, misalnya mengubah penutup lahan menjadi penggunaan lahan integrasi dengan SIG. di samping itu, kemampuan lay-out petanya termasuk paling bagus dibandingkan dengan peangkat lunak pengolah citra lainnya, miskipun belum sebagus perangkat lunak SIG vektor seperti Mapinfo Arcgis.
Hingga saat buku ini diterbitkan, kelemahan utama ILWIS ialah pada belum stabilnya perangkat lunak apabila dijalankan pada platfornm selain windos XP. Di samping itu, struktur datanya pun dalam versi yang baru relatif rumit dan kurang nyaman bagi pemula, miskipun satelah pemakaina cukup lama akan menimbulkan ketertarian yang mendalam untuk ekplorasi lebih jauh. Unuk pengolahan citra, ILWIS juga kurang cocok untuk proyek besar berukuran data yang sangat besar larena kecepatan pemrosesannya tidak sebaik ENVI,ER-Mapper dan Imagine.
Perangkat lunak lain yang mempunyai kemampuan integrasi pengolah citra dan SIG berbasis raster adalah idrisi (gambar 4.13). nama idrisi di ambil untuk menghormati al-idrisi, ahli geografi arab di abad ke 13.
Idrisi awalnya dikembangkan oleh departemen geografi di universitas clark, amerika serikat, dengan profesor ronald eastman sebagai projec leadernya. Idrisi sangat cocok digunakan pada proyek-proyek relatif kecil, meskipun kemampuan analisis spasialnya bisa di kategorikan unggul dan merupakan proyek eksperimen yang di lakukan oleh peneliti-peneliti besar di amerika. dari segi harga, idrisi merupakan yang paling murah di bandingkan perangkat lunak pengolah citra lainnya, kecuali di bandingkan ILWIS dan perangkat lunak open source lain.
Sebagai perangkat lunak pengolah citra dan SIG raster yang terintegrasi, indrisi menawarkan fasilitas dua sistem tersebut dengan proporsi yang kurang lebih sama. Kemampuan pengolah citra idrisi lebih baik dibandingkan ILWIS, bahkan terdapat fasilitas untuk analiasis hiperspektral serta klasifikasi berbasis objjek melaui teknis segmentasi citra. Dokumentasi melalui fasilitas bentuan pada modul/menu idrisi tersedia secara lengkap dan sangat bermamfaat, termasuk referensi teoritis yang digunakan, misalnya jurnal ilmiah yang digunakan sebagai basis pengembangan program.
Dengan idrisi, modul SIG berbasis raster secara umum bisa di jalankan dengan dua cara; melalui menu/kalkulasi peta berbasis aljabar citra/peta. Di samping itu, terdapat modul aplikasi SIG yang spesifik, misalnya analisis fragmentasi untuk aplikasi ekologi entang lahan dan juga permodelan perubahan penggunaan lahan, baik dengan pendekatan rantai markov maupun cellular automata. Kesemuanya terkait dengan data yang dipersiapkan melalui analisis citra. Modul lain yang serupa dengan ILWIS, namun dengan stabilan sistem yang lebih baik, adalah permodelan spasial berbasis data raster untuk analisis hidrologi dan erosi, misalnya miskipun demikian, fleksibilitas untuk analisis data dari luar menu tidak sebaik perangkat lunak pengolah citra dan SIG berbasis raster lainnya.
Berikut ini contoh beberapa perangkat lunak, baik yang bersifat komersial, gratis, maupun milik pemerintah, dengan kemampuan untuk pengolahan citra dan integrasinya dengan SIG. tabel 4.5 berikut merupakan moditifikasi atas jensen (2005).
DAFTAR PUSTAKA
Danoedoro.p. 2012 Pengantar Penginderaan Jauh Digital. Yogyakarta: Andi
























Tidak ada komentar:
Posting Komentar