BAB 6 PENAJAMAN CITRA DAN PEMFILTERAN SPASIAL
Penajaman citra (image enhancement)
meliputi semua operasi yang menghasilkan citra ‘baru’ dengan kenampakan visual
dan karakteristik spektral yang berbeda. Di samping penajaman citra, ada lagi
jenis operasi yang disebut pemfilteran (filtering). Pada beberapa pustaka
(misalnya Niblack, 1986; dan Mulder dan Kostwinder, 1987) kedua teknik ini
tidak dikelompokan dalam satu kelompok operasi yang disebut penajaman citra.
Pada umumnya para penulis yang mempunyai latar belakang bukan ilmu kebumian
cenderung mengelompokan pemfilteran sebagai teknik terpisah dari teknik-teknik
penajaman karena efek yang dihasilkan dan filosofinya pun berbeda dari
teknik-teknik penajaman yang lain. Namun ada pula beberapa penulis yang
menyatukan teknik penajaman dan pemfilteran sebagai satu kelompok operasi
penajaman.
6.1 PENAJAMAN KONTRAS
Penajaman
kontras (contrast enhancement) diterapkan untuk memperoleh kesan kontras citra
yang lebih tinggi. Hal ini dapat dilakukan dengan mentransformasi seluruh nilai
kecerahan dan memberikan hasil berupa citra dengan nilai maksimum baru yang
lebih tinggi dari nilai maksimum awal, dan nilai minimum baru yang (pada
umumnya) lebih rendah dari nilai minimum awal. Secara visual, hasil ini berupa
citra baru yang variasi hitam-putihnya lebih menonjol sehingga tampak lebih
tajam dan memudahkan proses interpretasi. Algortitma penajaman kontras ini
dapat di kelompokan menjadi dua, yaitu perentangan kontras (contrast
stretching) dan ekualisasi histogram (histogram equalization). Masing-masing
algoritma dijelaskan sebagai berikut ini.
6.1.1 Perentangan Kontras
Kontras citra
dapat dimanipulasi dengan merentang nilai kecerahan pikselnya. Perentangan yang
efektif dapat dilakukan dengan memperhatikan bentuk histogramnya. Citra asli,
yang biasanya mempunyai julat nilai lebih sempit 0-255, perlu direntang
sehingga kualitas citranya menjadi lebih baik. Hasil perentangan ini adalah
citra baru, yang bila digambarkan histogramnya berupa kurva yang lebih lebar
(lihat Gambar 6.1)
Terdapat
beberapa cara untuk merentang kontras citra. Cara paling sederhana ialah dengan
mengalikan citra tersebut, misalnya dengan faktor pengali p. Citra X dengan julat nilai kecerahan 0-21, bila dikalikan dengan
faktor p = 3 menghasilkan citra X’
dengan julat 0-63. Pada pengaturan warna hitam-putih, citra baru ini akan
tampak lebih kontras karena julatnya semakin lebar. Nilai maksimum lama, yaitu
21, yang tampak gelap ditransformasi manjadi nilai maksmimum baru, 63, yang tampak
jauh lebih cerah; sedangkan nilai minimum dijaga tetap (Gambar 6.2.a)
Cara lain adalah
suatu pengondisian. Perentangan dilakukan pada julat diantara nilai maksimum
dan nilai minimum. Misalnya citra X {0..21} akan direntang menjadi citra X”
{0..255}, tetapi dengan mengambil nilai 3 sebagai nilai masukan minimum dan 19
sebagai nilai masukan maksimum. Dalam hal ini, nilai asli pada citra X {0..21}
yang <= akan menjadi 0 pada citra baru, dan nilai asli yang >= 9 akan
menjadi 255 (gambar 6.2.b).Transformasinya adalah sebagai berikut :
BV output = (BV
input – BV min) / (BV maks – BV min) *
255 ................................. (6.1)
BV output
adalah nilai kecerahan baru hasil transformasi, BV input adalah
sembarang nilai kecerahan piksel pada citra yang menjadi masukan, BV maks
adalah nilai kecerahan maksimum piksel pada citra asli. Nilai koefisien 0-255
(kecerahan maksimum). Apabila menghendaki nilai maksimum piksel hasil
transformasi sebesar 200 maka nilai 255 tersebut dapat diganti dengan 200. Pada
persamaan ini, jika BV output ternyata negatif maka nilai baru akan
diatur menjadi sama dengan 0. Begitu pula
apabila BV output > 255 maka nilai baru akan diatur
menjadi 255.
Operasi
perentangan kontras ini dapat dibalik sehingga menghasilkan citra baru yang lebih
sempit julatnya dan disebut sebagai pemampatan kontras (contrast compression).
Baik perentangan maupun pemampatan kontras mengubah nilai kecerahan piksel satu
demi satu, tanpa melibatkan nilai piksel yang berdekatan (piksel tetangga).
Oleh karena itu, operasi ini disebut sebagai operasi global, yang secara
konseptual berbeda dengan operasi lokal atau operasi fokal (ketetanggaan)
melalui teknik pemfilteran. Pada kebanyakan perangkat lunak pengolah citra
untuk keperluan publishing, biasanya citra ditampilkan sudah dalam keadaan
terentang dengan menggunakan nilai default 1% atau 2%. Nilai default ini pun
biasanya dapat diubah sesuai dengan kebutuhan analis.
Gambar 6.2 Perentangan
Kontras Secara Linier dengan menggunakan masukan nilai minimum dan maksimum asli
maupun nilai piksel pada posisi presentase komulatif tertentu (Sumber , Jensen,
2005 dengan Perubahan)
Gambar 6.3 Atas : Citra
asli Landsat Thematic Mapper wilayah Semarang saluran 3 (merah); bawah : citra
dipertajam melalui teknik perentangan kontras secara linier dengan cut-off dan saturation 1%.
6.1.2 Ekualisasi Histogram
Teknik penajaman
kontras yang telah diuraikan diatas adalah suatu teknik penajaman kontras
linier. Selain linear stretching ini,
ada lagi teknik penajaman dengan cara ekualisasi histogram ini dapat dibagi
menjadi tiga tahap. Pertama, dilakukan penghitungan untuk menurunkan histogram
citra yang akan dipertajam. Kedua, si operator kemudian menentukan jumlah kelas
kecerahan yang baru (misalnya 32). Data BV seluruh cutra nantinya akan
didistribusikan kembali ke masing-masing kelas tersebut. Ketiga, program akan
menghitung dan menandai piksel demi piksel, untuk kemudian mengelompokan mereka
masing-masing dalam jumlah yang kurang lebih sama ke tiap kelas kecerahan yang
tersedia. Setelah itu, dengan sendirinya citra baru (atau tampilan pada layar)
segera dihasilkan.
Ekualisasi
histogram menghasilkan citra dengan kontras maksimum bila pengambilan julat
nilai kecerahannya tepat seperti halnya pada perentangan kontras linier.
Pengambilan ini dikatakan tepat bila julat nilai tersebut mewakili populasi
terbanyak dalam histogram (misalnya pada ‘bukit’ kurva utamanya).
Tabel 6.1
Statistik untuk citra hipotetik 64 kolom x 64 baris (4096 piksel) dengan julat
BV 0-7 (8 bit)
Nilai Kecerahan
|
Frekuensi
|
0
|
790
|
1
|
1023
|
2
|
850
|
3
|
656
|
4
|
329
|
5
|
245
|
6
|
122
|
7
|
81
|
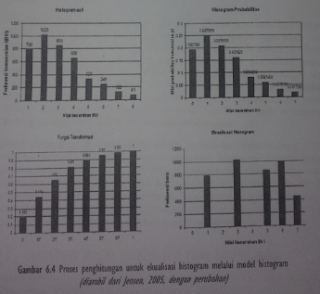
Berikut ini
uraian singkat yang diambil dari Jensen (2005, yang juga merupakan modifikasi
atas contoh yang dibuat oleh Gonzalez dan Wintz, 1977). Misalkan terdapat suatu
citra hipotetik yang terdiri atas 64 kolom x 64 baris (total = 4096 piksel)
dengan julat nilai 0-7 (BV,=8). Histogram dan distribusi frekuensinya dapat
dilihat pada gambar 6.4a dan tabel 6.1. disana terlihat bahwa piksel dengan
nilai 0 berjumlah 790 (fBV0 = 790), kemudian fBV1 = 1023,
dan seterusnya. Probabilitas kemunculan tiap nilai kecerahan pBvi pun
dapat dihitung dengan cara membagi tiap frekuensi BVi dengan jumlah
piksel total (n=4096). Rinciannya dapat dilihat pada tabel 6.1.
Setelah itu,
dibuat histogram yang menyatakan distribusi frekuensi nisbah nilai kecerahan BVi
terhadap BV maksimum (dari 0,1/7, 2/7, 3/7, .., 1) pada gambar 6.4b. histogram
ini kemudian ditransformasi menjadi histogram kumulatif pada gambar 6.4c.
berdasarkan histogram kumulatif ini, fungsi transformasi probabilitas si dibuat,
yang menyatakan nilai kumulatif probabilitas tiap nisbah (rasio) kecerahan
(lihat gambar 6.4d). formulasinya adalah si = pi, i = 0, 1,2,3,..
Tahap terakhir
adalah pengelompokan kembali nilai kecerahan berdasarkan nilai
tertransformasi si . contoh
ini dimulai dari nilai s0 = 0.19 , yang lebih dekat ke nilai penisbahan
0.14 (hasil transformasi BV1) sehingga seluruh piksel bernilai 0
ditransformasi bernilai 1. Beralih ke nilai si = p0+pi = 0.19+0.25 =0.44. Nilai
ini lebih dekat ke nilai penisbahan 3/7 (=0.43), yang dimiliki oleh BV3
sehingga seluruh piksel bernilai 1 ditransformasi menjadi bernilai 3. Begitu
seterusnya hingga diperoleh nilai baru 5 untuk piksel asli bernilai 2, dan
nilai baru 6 untuk nilai asli 3 dan 4, serta nilai baru 7 untuk nilai asli 5,6
dan 7. Nyata bahwa nilai kecerahan asli 0,2, dan 4 tak dipresentasikan lagi.
Hasilnya adalah citra baru kekontrasannya lebih optimal.
Penajaman
kontras merupakan teknik manipulasi dasar dalam studi pengindraan jauh. Hampir
semua operasi ekstraksi informasi membutuhkan bantuan teknik ini, sejauh hasil
proses tersebut digunakan sebagai materi utama pemilihan sampel (misalnya dalam
penyusunan komposit yang baik untuk klasifikasi multispektral), delineasi
satuan-satuan pemetaan pada hasil cetak (hard copy), dan sebagainya. Penajaman
kontras atas citra saluran-saluran asli tidak pernah direkomendasikan, apabila
saluran-saluran tersebut akan digunakan sebagai masukan dalam proses
klasifikasi
Multispektral,
penisbahan saluran (band rationing), transformasi indeks vegetasi, ataupun
transformasi lain seperti halnya principal component analisis (PCA) ataupun
transformasi tasseled-cap dari kauth dan thomas (lihat bab 7).
Dalam
penajaman citra yang membutuhkan informasi mengenai variasi penutup/penggunaan
lahan pada suatu citra, teknik perentangan kontras lebih disukai karena mampu
menghasilkan kenampakan gradual nilai-nilai pixel yang berdekatan. Apabila
teknik ini diterapkan pada saluran-saluran tampak, maka akan jelas terlihat
variasi jenis penutup lahan termasuk didalamnya perbedaan kerapatan vegetasi
pada lahan-lahan pertanian. Begitu pula halnya dengan kenampakan tubuh air
dengan gradiasi kekeruhannya, yang mengindikasikan besarnya muatan tersuspensi.
Apabila
kenampakan blok antar objek lebih dibutuhkan, misalnya pengenalan zona-zona
permukiman dengan pemisah berupa jaringan jalan yang ingin dipertegas, maka
teknik ekualisasi histogram pada umumnya lebih eksprisif. Penggunaan teknik ini
untuk mempertegas perbedaan antara tubuh air dan vegetasi pada saluran
inframerah dekat (XS3 SPOT DAN TM4 Landsat) lebih di anjurkan. Lebih dari itu,
kadang-kadang diperlikan juga suatu kombinasi teknik penajaman kontras dengan
teknik pemfilteran, karena citra hasil pemfilteran pada umumnya kurang mampu
menyajikan kekontrasan secara tepat.
Perlu
ditegaskan disini bahwa penajaman kontras tetap tidak mampu menekan
pengarug/gangguan atmoefer,, khususnya apabila gangguan tersebut terjadi secara
tiadak merata. Liputan citra yang sacear parsial tergantung oleh kabut tipis
akan lebih efektif dikoreksi degan model transfer atau meleui kalibrasi garis
impiris, seperti yang telah diuraikan pada bab5. Penajaman kontras terhadap
citra semacam ini justru akan mempertajam kenampakan gangguan atmosfernya.
6.3 PENAJAMAN SPASIAL
MELAUI FUSI CITRA MULTIRESOLUSI
Dalam
seperempat abad terakhir banyak sistem pencitraan telah menghasilkan citra
multispektral dan citra pankronatik. Secara umum dapat dikatakan bahwa suatu
sistem sensor yang mampu menghasilkan citra multispektral denngan resolusi
spasial tertentu akan memberikan citra
Pankromatik
dengan resolusi spasial yang lebih tinggi. Hal ini wajar, mengingat dengan
menggunakan lebar spektrum yang lebih besar, sensor dan detektor dapat
mengumpulkan energi dengan nisbah sinyal terhadap derau yang lebih besar untuk
luasan area yang lebih sempit. Oleh karena itu, apabila suatu sensor dengan
saluran spektral berjulat spektrum relatif sempit memerlukan area seluas 20x20
m kuadrat, maka dengan saluran spektral pankromatik (0,51-073 um) hanya
memerlukan area area yang lebih sempit, misalnya seluas 10x10 m kuadrat atau
kurang untuk mengumpulkan energi yang kemudian dikonversi ke nilai kecerahan
pixel.
SPOT
1-3 merupakan salah satu sistem satelit pertama yang mampu menghasilkan citra
multispektral (resolusi spasial 20 m) dan pankromatik (15 m). SPOT 5, ikonos,
quickbird, orbview, geoeye merupak contoh satelit yang menghasilkan citra
multispektral dan pankromatik yang jauh lebih tinggi, yaitu 2,5 hingga 0,5 m.
Ide
pengubahan citra multispektral dan pankromatik kemudian muncul yang kemudian
disebut resolusi pan-sharpened colour composite, alasannya miskipun mempunyai
resolusi spasial lebih tinggi, citra pankromatik pada umumnya kurang menarik
untuk dimamfaatkan secara mandiri karena tidak ada unsur warna dalam
visualisasinya. Oleh karena itu, suatu metode yang dapat mengombinasikan
keunggulan multispektral dalam aspek warna, dengan keunggulan citra pankromatik
dalam aspek kerincian spasialnya karena resolusi spasial yang lebih tinggi
dikembangkan. Panggambungan ini menghasilkan citra multispektral yang tetap
berwarna-warni dan dipertajam secara spasial oleh citra pankromatik.
Ada
beberapa macam metode penggambungan citra multispektral dan pankromatik, namun
semuanya sebenarnya bertumpu pada metode berbasis aljabar citra, yang
menyaratkan ko-registrasi spasial pada semua citra masukan. Pada awalnya metode
penggabungan ini hanya diterepkan pada citra multispektral yang terdiri dari 3
saluran, untuk dipadukan dengan 1 citra pankromatik (short, 1982).
6.3.1
metode perkalian (multiplikatif)
Metode
perkalian (multiplikatif) merupakan metode paling sederhana. Melalu metode ini,
setiap citra saluran multispektral dikalikan dengan citra saluran pankromatik. Perkalian ini melibatkan
proses aljabar peta yang mensyaratkan ko-registrasi, dimana citra multispektral
secara otomatis di resample sehingga menghasilkan citra baru yang merupakan
kombinasi citra masing-masing saluran multispektral dengan pankromatik. Yang
julat nilai pixelnya diskalakan menjadi ke 0-225. Penyusunan citra komposit
dilakukan dengan menggunakan masukan setiap saluran spektral baru, yang telah
terkombinasi dengan citra pankromatik.
Kelemahan
utama metode multiplikatif adalah ketidakmampuan untuk mempertahankan untuk
mempertahankan aspek radiaometri multispektral. Miskipun demikian, banyak kasus
dalam menggunakan metode ini masih mampu menonjolkan kenampakan yang terkait
dengan fenomena kekotaan. Karena adanya peningkatan intensitas sebagai hasil
dari operasi lain.
6.3.2 METODE
TRANSFORMASI BROVEY
Merupakan
metode yang paling populer untuk memedukan dua macam citra yang berbeda
resolusi spasial. Transformasi brovey mengubah nilai spektral asli pada setiap
saluran multi spektral, katakanlah berkode saluran merah (M), hijau (H), biru
(B). menjadi saluran-saluran baru (MP, BP,HP) yang masing-masing telah diperinci
secara spasial oleh citra pankromatik dan di normalisasikan nilai kecerahannya
dengan mempertimbangkannya nilai-nilai pada saluran lainnya. Rumusnya adalah
sebagai berikut (short 1982, vrabel 1996).
Melalui
metode ini secara otomatis ketiga saluran spektral M,H dan B akan di resample
ke ukuran pixel saluran P, baik menggunakan nearest neighbour, bi-linear,
ataupun cubic convolution.
6.3.3 METODE
GRAN-SCHIDT
Metode
ini digunakan oleh perangkat lunak ENVI, tetapi juga digunakan oleh perangkat
lunak IDRISI dengan nama lain, yaitu transformasi regresi lokal. Liu dan mason
(2009) menamakannyamodulisasi intensitas berbasis filter penghalusan, serta
menjadi dasar bagi penjelasan berikut ini. Dengan demikian, istilah
gram-schmidt, tranformasi regresi lokal dan SFIM sebenarnya mengacu ke metode
yang sama, yang bertumpu pada hasil penelitian price (1999).
Metode
SFIM dikembangkan berdasarkan alasn bahwa fusi citra multi resolusi, misalnya
transformasi HIS dan brovey, dapat menyebabkan distorsi warna apabila julat
spektral dari citra pengganti intensitas yang biasanya diwakili oleh citra
penkromatik beresolusi tinggi, berbeda dari ketiga saluran multispektral yang
akan diperbaiki tampilan spasialnya. Masalah semacam ini akan semakin menonjol
ketika kedua macam tidak diperoleh pada tanggal yang sama. Tampilan yang sangat
mengganggu ini biasanya muncul pada wilayah bervegetasi karena adanya perbedaan
masa tanam di wilayah pertanian.
Secara
garis besar, penajaman spektral SFIM melibatkan empat langkah berikut. Pertama,,
melakukan simulasi saluran pankromatik resolusi tinggi berdasarkan saluran
multispektral dengan resolusi spasial lebih rendah, transformasi gram-schmidt
diterapkan pada saluran pankromatik hasil simulasi dan saluran multispektral,
dimana saluran pankromatik hasil simulasi siperlakukan sebagai saluran pertama.
Ketiga, saluran pankromatik resolusi tinggi yang asli kemudian digantikan oleh
saluran gram-schmidt hasil simulasi. Ke empat, transformasi gram schmidt
dabalik untuk diterapkan, membentuk saluran-saluran multispektral yang
dipertajam dengan saluran pankromatik.
Model
SFIM atau gram schmidt dilandasi oleh model radiasi matahari. Mengacu ke
penjelasan liu dan mason (2009), nilai pixel suatu citra optik yang diambil di
siang hari ditentukan oleh dua faktor, yaitu radiasi sinar matahari yang
mengenai permukaan bumi, yaitu irradiansi, dan pantulan dari permukaan bumi.
Apabila
BV mewakili nilai pixel citra rendah berolusi lebih rendah dan mewakili nilai
pixel citra berolusi lebih tinggi. Maka ko-regrestrasi citra resolusi rendah
mengacu ke citra resolusi tinggi akan menyebabkan setiap pixel pada citra
resolusi rendah harus diperbesar sekian kali, sesuai dengan rasio antar kedua
macam resolusi. Misalnya, resolusi rendah adalah 20 m dan resolusi tinggi adalah
10 m maka rasio kedua adalah 20:10=2 (artinya setiap satu pixel resolusi rendah
memuat 2x2=4 pixel resolusi tinggi).
Dalam
model SFIM diperlukan simulasi citra resolusi tinggi dengan niali pixel BV yang
digunakan nilai rerata pada ke empat nilai pixel asli BV. Satu nilai baru yang
menggantikan ke empat nilai pixel resolusi rendah ini diperlu didefinisikan
dengan menggunakan prisip rerata lokal yang memperhatikan ke empat pixel
resolusi tinggi yang menyusun satu pixel resolusi rendah.
Nilai
pixel pada citra SFIM didefinisikan
sebagai;
Dari
perspektif model radiasi mataharii, irradiansi yang mengenai permukaan bumi
dikontrol oleh topografi. Apabila dua macam citra dikuantifikasikan pada satu
resolusi spasial, karena keduanya bervariasi sebagai efek dari kontrlo
topografi yang serupa. Selanjutnya p rendah= p tinggi apabila tiadak ada
variasi spektral signifikan pada pixel-pixel pengyusun BV. Dengan demikian
dalam persamaan
E
rendah dan E rendah akan saling meniadakan, sementara p rendah dan p tinggi
juga saling meniadakan. E tinggi dapat digantikan oleh E tinggi akhir, rumus
diatas bisa digantikan oleh rumus yang lebih sederhana sebagai berikut;
Dimana
citra resolusi rendah adalah saluran tertentu beresolusi lebih rendah yang di
registrasikan keseluruh dengan resolusi spasial lebih tinggi. Citra rerata
lokal adalah saluran baru yang diperoleh degan cara menerapkan pemfilteran
rerata=nilai rasio antara resolusi tinggi terhadap resolusi rendah, misalnya 20
m terhadap 10 m memberikan rasio 2, dan ukuran filter menjadi 2x2. Cara
menerapkan pemfilteran bisa dibaca di sub bab 6.4.
Dimana
tiga saluran rendah adalah saluran tertentu beresolusi yang akan diberi merah,
hijau dan biru melalui fusi dengan saluran pankromatik, maka rumus di atas
menjadi;
Miskipun
liu dan mason (2009) menegaskan bahwa model SFIM inimampu mempertahankan aspek
spektral dalam fusi citra multiresolusi, ada juga kelemahannya yang sangat
dipengaruhi oleh akurasi geometri. Kelemahan ini muncul ketika citra
multispektral resolusi rendah tidak teregistrasi atau terkoreksi geometri
dengan baik, mengacu ke citra berresolusi lebih tinggi, maka pergeseran posisi
ini akan muncul dalam bentuk gangguan warna.
6.3.4 METODE PRINCIPAL
COMPONENT
Metode
penajaman spasial melaui fusi citra multispektral dengan citra pankromatik juga
dapat dilakukan dengan metode principical component analisis (PCA). PCA
merupakan suatu analisis data multispektral dengan jumlah saluran relatif
banyak, untuk menghasilkan citra baru dengan jumlah saluran yang lebih sedikit,
kandungan informasi yang dimilikinya mewakili sebagian besar infoermasi dari
citra saluran-saluran asli. Saluran baru berupa citra PCI hasil transformasi
PCA citra lansat ETM+ misalnya, bisa memuat hingga 83% dari total informasi ke
enam saluran. PC2 bisa mencapai hingga 14 %, dan presentase ini akan semakin
sedikit pada PC-PC berikutnya. Pembahasan lebih lanjut untuk PCA bisa dibaca
pada bab 7 dan sub bab 7.5.
Penggunaan
teknik PCA untuk fusi dua macam citra berbeda resolusi spasial dan spektral,
mengikuti langkah-langkah berikut. Pertama, citra multi spektral ditransformasi
dengan PCA sehingga menghasilkan citra baru dengan nama PC1,PC2,PC3 dan
seterusnya. Berangkat dari asumsi bahwa citra
PG1 mewakili sebagian besar informasi pada saluran multispektral asli
dan bahwa PC1 tersebut hanya mengandung iluminasi scene total, sementara
variasi antar saluran di kandung oleh PC-PC yang lain (welch dan ehlers, 1987;
bretschneirder dan kao, 2000).
Gambar 66. Contoh tampilan di perangkat lunak ERDAS
Imagine yang menyediakan menu penajaman
spasial melalui fusi data multiresolusi
Kedua , citra PC1 kemudian di ganti oleh
citra pangkromatik resolusi tinggi melalui prosesre – mapping julat numerik citra pangkromatik agar sama dengan
julat numerik PC1. Ketiga, setelah himpunan data PC berganti anggota , dimana
PC1 digantikan oleh citra Pangkromatik
resolusi tinggi maka seluruh PC dalam
satu himpunan data PCA itu di resample ke
resolusi tinggi, mengikuti citra pangkromatiknya , keempat seluruh data PC
dalam satu himpunan di transformasi kembali (inversely transformed) untuk menghasilkan kembali citra saluran –
saluran multispektral penyusunnya, namun masing – masing saluran sudah memuat
informasi intensitas dan resolusi spasial
citra pangkromatik.
6.3.5.
Metode Normalisasi Warna ( CN )
Penajaman
spektral dengan metode normalisasi warna (Colour
Sharpening atau Colour Normalization,CN ) sebenarnya merupakan perluasan
dari metode Brovey. Perluasan ini terletak pada kemampuannya melibatkan lebih
dari tiga saluran. Jadi dengan kata lain, CN mampu mentransformasi
&mempertajam saluran multispektral
dengan jumlah berapa pun untuk di padukan dengan citra pangkromatik dengan
resolusi spasial yang lebih tingggi. Algoritma yang ada pada CN mampu
mempertahankan tipe data pada citra masukan beserta julat spektralnya. CN juga
dapat diterapkan pada citra hiperspektral untuk di pertajam dengan citra
multispektral beresolusi spasial lebih tinggi.
Penajaman
spektral dengan metode CN juga di sebut energy
subdivision transform karena menggunakan penajaman spasial citra
multispektral berdasarkan citra dengan resolusi spasial tinggi namun sekaligus memiliki resolusi spektral rendah .
julat spektral citra resolusi spektral
rendah ( lebar) yang di gunakan harus mencakup seluruh julat spektral saluran –
saluran citra spasial rendah yang akan di pertajam secara spasial. Apabila
terdapat saluran – saluran spektral di luar julat minimum – maksimum citra
resolusi spasial tinggi maka saluran akan tetap tak berubah ( tak di pertajam
). Julat spektral citra yang digunakan untuk mempertajam di definisikan dengan
pusat panjang gelombang dan nilai
minimum setengah lebar spektral penuh. Data semacam ini di asumsikan sudah ada
di header citranya & masing – masing citra masukan sudah di
definisikan lebar spektral maupun pusat nilai panjang gelombangnya.
Dalam proses spasial melalui CN ini , semua saluran masukan di kelompokan ke
dalam segmen – segmen spektral yang didefinisikan oleh julat spektral
beresolusi tinggi dan hasilnya di normalisasi yaitu di bagi dengan jumlah total
citra masukan yang termasuk dalam segmen.
Rumus
CN adalah sebagai berikut ( Liu & Mason , 2009 ) :
6.4. PEMFILTERAN
SPASIAL
Pemfilteran ( spatial filtering ) sebenarnya merupakan kelompok operasi
tersendiri dan bukan hanya penajaman, Swain & Davis (1978) memberikan batasan filter sebagai mekanisme
yang dapat mengubah sinyal – sinyal optis,elektronis ataupun digital, sesuai
dengan kriteria tertentu lebih lanjut, keduanya menyatakan bahwa pemfilteran
adalah suatu cara untuk ekstrasi bagian data tertentu dari suatu himpunan data
, dengan menghilangkan bagian – bagian data yang tidak di inginkan .
Perlu
ditegaskan bahwa pengertian filter dalam pengolahancitra berbeda dengan pengertian
filter dalam fotografi. Persaman mendasar keduanya hanya terletak pada kemampuan untuk ‘menyaring’ atau menapis
informasi sehingga menghasilkan informasi selektif yang tak dapat di lihat pada
kondisi biasa. Filter fotografi yang
lebih dikenal sebagai filter optis mampu menapis beberapa spektrum panjang
gelombang dan juga melanjutkan spektrum tertentu. Filter dalam pengolahan citra
( secara khusus di sebut filter digital)
dirancang untuk ‘menyaring’ infor-masi spektral sehingga menghasilkan citra
baru yang mempunyai variasi nilai spektral yang berbeda dari citra asli.
6.4.
1 Filter Konvolusi dengan Jendela Bergerak
Berbeda halnya dengan teknik penajaman
kontras , operasi pemfilteran diterapkan dengan mempertimbangkan nilai piksel
yang bertetangga. Oleh karena itu , teknik pemfilteran lebih sering di sebut
sebagai operasi lokal (local operation),
sedangkan teknik penajaman yang lain di sebut operasi titik (point operation) (Galtier, 1989).
Operasi lokal ini dapat dilakukan dengan menerapkan alogaritma moving window ,Jendela yang dimaksud
disini adalah matriks, biasanya 3 x 3
atau 5 x 5 , 7 x 7 dan seterusnya, yang dioperasikan terhadap matriks total ( i
baris x j kolom citra ), melaui algoritma tertentu sehingga menghasilkan nilai
baru pada posisi nilai piksel pusat. Nilai baru ini
menggantikan nilai lama . setelah itu , jendela di geser lagi ke posisi
berikutnya ( ke kanan ) sampai satu baris selesai , dan di lanjutkan lagi ke
baris selanjutnya sampai seluruh citra selesai di hitung.
Tiap
jendela matriks mempunyai nilai atau bobot sendiri , begitu pula algoritmanya,
khususnya untuk jendela yang berbentuk 3 x 1 ataupun 2 x 2. Dalam paket program
pengolahan citra, penyusunya jendela matriks ini dapat sangat interaktif
sehingga pengguna dapat mengisikan nilai sesuai dengan keinginan ke dalam tiap
sel matriks tersebut.
Terdapat bermacam macam filter digital ,
tetapi dalam konteks penajaman citra terdapat dua macam filter utama , yaitu
filter high–pass dan fiter low-pass, Keduanya menghasilkan efek
yang berlawanan. Fiter high-pass
menghasilkan citra dengan variasi nilai kecerahan yang besar dari piksel ke
piksel , sedangkan fiter low-pass justru berfungsi sebaliknya. Di samping itu, masih lagi kategori filter lain , yang
tidak akan di uraikan disini secara panjang lebar.
Untuk membahas
filter, terlebih dahulu kita ketahui pengertian frekuensi nilai keceraha. Bila
kita membuat penampang melintang diatas sebuah citra digital, kita akan
memperoleh informasi nilai kecerahan (BV) dari suatu piksel ke piksel
berikutnya . semvkin besar variasi nilai dari suatun piksel ke piksel
selanjutnya , di katakan semakin tinggi frekuensinya ( lihat gambar 6.8 dan
6.9).
Penggunaan
filter high-pass ialah untuk menaikan
frekuensi ini sehingga batas satu bentuk dengan bentuk lain menjadi semakin
tajam. Penggunaan filter low-pass
adalah untuk menghasilkan efek kebalikannya : batas suatu bentuk ke bentuk lain
menjadi kabur sehingga terkesan gradasi yang halus. Gradasi yang halus inilah
yang di sebut dengan frekuensi rendah.
1.
Penggunan Gain dan Offset
Pada setiap matriks
filter terdapat koefisien Ci yang
dapat di ubah – ubah oleh operator. Bagaimana kita bisa membedakan suatu filter
bersifat high-pass dan yang lain
bersifat low-pass ? ada beberapa cara
untuk melakukan hal tersebut, namun berikut ini hanya di jelaskan salah satu
cara yang paling sederana , yaitu pengunaan gain
dan offset. Berikut ini di berikan
Contoh salah
satu matriks filterberukuran 3 x 3
dengan koefisien matriks Ci untuk i = 1,2,3....9,
Besarnya gain didefinisikan sebagai :
dan untuk
mengindari nilai tak terhingga karena penyebut bernilai 0 maka program biasanya
mengatur apabila jumlah total seluruh koefisien dalam matriks bernilai 0,nilai gain diatur menjadi 1.
Matriks ini di
gunakan untuk mengubah nilai piksel pada citra, tepat yang berimpit dengan Cs melalui perkalian nilai gain dengan jumlah dari hasil kali
setiap nilai koefisien filter Ci dengan
nilai piksel BV pada posisi yang sama pada citra :
Dimana BVpusat_baru
adalah BV5 ( pada posisi
kelima dalam kernel 3 x 3 ) atau BV13
(pada posisi
ketiga belas dalvm kernel 5 x 5). Besarnya Offset
bervariasi antara 0-255, yang gunanya ialah untuk ’ menggeser’ nilai kecerahan
citra menjadi lebih tinggi. Offset akan
sangat bermanfaat apabila hasil kali gain dengan jumlah perkalian setiap
koefisien dengan nilai piksel pada citra bernilai negatif atau sangat rendah
sehingga tampak gelap pada layar monitor.
Berdasarkan
formulasi ini , pemberian nilai
koefisien yang berbeda- beda akan memberikan efek spasial yang berbeda
pula. Misalnya, apabila semua keofisien bernilai + 1 maka akan dihasilkan efek
spasial yanb berbeda jika c5 diberi nilai 9 dan koefisien sisanya di beri -1.
2.
Filter
Low-pass
Filter ini
paling sering di gunakan untuk memperhalus kenampakan citra.
Biasanya
berbentuk jendela matriks 3 x 3 ataupun 5 x 5 yang tiap selnya berisi nilai
integer dengan perbedaan nilai yang tidak terlalu besar.
Moving average filter atau mean fiter menghasilkan kenampakan
halus, dimana nilai piksel yang barumerupakan rerata dari hasil kvli tiap
elemen matriks dengan nilai piksel yang dimaksud.
Bila mean filter ini dioperasikan terhadap
citra asli-hipotetik seperti diatas maka filter ini akan mulai dari susunan
piksel pojok kiri atas ( lihat gambar ). Apabila nilai offset diberi 0 maka nilai 13 sebagai nilai asli akan
tertransformasi kembali menjadi :
Nilai 28 ini
adalah nilai rerata dari sembilan piksel yang bertetangga, setelah
‘menyelesaikan’ jendela ini, matriks bergeser ke jendela berikutnya, yaitu.
13 12 20 .
. . .
13 10 9 . .
. .
50 50 51. .
.
Bila
diperhatikan terdapat dua gejala yang penting hasil pemfilteran dengan filter low pass ini. Gejala pertama ialah terjadinya penghalusan (smoothing) gradasi
nilai dari satu piksel ke piksel yang lain sehingga perubahan nilai yang
mencolok dapat ditekan dengan memberikan nilai baru yang merupakan rerata dari
niali-nilai piksel tetangga. Gejala kedua yaitu pada hasil pemfilteran terjadi
penyusutan ukuran asli citra, dari m kolom x n baris menjadi m-2 kolom x n-2
baris untuk filter berukuran 3x3; m-4 kolom x n-4 baris , untuk 5x5; dan
seterusnya. Untuk menghindari penyusutan ukuran citra yang terfilter; biasanya
pada program pemfilteran ditambahkan suatu algoritma penyalinan baris-baris
kedua dari atas dan kedua dari bawah untuk mengganti baris –baris yang hilang,
yaitu baris teratas dan terbawah. Hal yang sama diterapkan pada kolom-kolom
yang hilang sehingga ukuran citra terfilter menjadi sama dengan ukuran citra
asli.
Karena efeknya
yang menghaluskan citra, algoritma pemfilteran ini disebut juga sebagai algoritma
smoothing(penghalusan). Algoritma smoothing yang lain ialah menggunakan filter
semacam ini:
3. filter high-pass
Filter high-pass
biasa digunakan untuk menonjolkan perbedaan antara objek ataupun perbedaan
nilai, kondisi ataupun sifat antar objek yang diwakili oleh nilai piksel.
Perbedaan ini dapat ditonjolkan melalui teknik penajaman tepi(edge enhancement)
dan juga penonjolan kenampakan linear. Penajaman tepi sangat baik untuk
menyajikan kenampakan objek yang sangat bervariasi pada citra sehingga satu
sama lain dapat dibedakan degan mudah. Filter-highpass juga diterapkan dalam
penyajian efek bayangan (shadow effect) sehingga mempermudah analisis
fisiografik. Filter high pass meliputi berbagai operasi lokal yang mempertajam
kesan. Namun dapat dikelompokan menjadi tiga. Perhatikan pembahasan berikut.
4.Filter dengan metode subtraksi
ada tipe filter gradien ,perbedaan intensitas atau nilai kecerahan dapat dihitung pada arah sumbu x dan y . perbedaan ke arah x dapat di hitung sebagai berikut:Prosedur penurunan citra baru melalui filter high pass pengurangan (subtraksi) ini dapat dibagi menjadi dua langkah. Pertama penghitungan nilai baru dengan menggunakan algoritma moving average berdasarkan definisi matriks filternya. Kedua citra high pass diperoleh dari pengurangan citra asli dengan citra moving average nya (shresta,1991)
5.filter gradien
Pada tipe filter
gradien ,perbedaan intensitas atau nilai kecerahan dapat dihitung pada arah
sumbu x dan y . perbedaan ke arah x dapat di hitung sebagai berikut :
Pemfilteran ini
dapat pula diterapkan untuk pembuatan model tiga dimensi dengan DTM . berbeda
dengan filter-filter yang telah diuraikan terdahulu, filter arah (directional
filter) ini di terapkan pada data digital hasil interpolasi kuntur. Citra
kontur hasil intelpolasi garis-garis isoline dipandang sebagai citra intensitas
dan difilter sehingga menghasilkan dua citra turunan (derivat) yaitu citra arah
x dan citra arah y.
Namun disamping
kearah sumbu x dan y , penajaman pun dapat diagonal melalui filter berikut:
6.filter lapalce
Filter lapalce
merupakan filter yang di dasari oleh derivatif kedua drivatif pertama
memberikan gradien , sedangkan memberikan gradien , sedangkan derivatif kedua menghasilkan laju perubahan gradien.
Hasil berupa nilai positif menujukan
penambahan laju perubahan dan hasil nilai negatif menunjukan pengurangan laju
perubahan. Nilai 0 menunjukan sifat konstan. Bila diterapkan pada citra. Filter
lapalce ini secara langsung aka menunjukan efek
yang cenderung diperhalus (smoothed). Sedangkan bila hasil tersebut dijadikan
pengurangan , efek yang dihasilkan adalah penajaman tepi (shresta 1991).
6.4.2 filter mayoritas
Filter mayoritas
pada dasarnya bukan suatu algoritma penajaman dan tidak memberikan efek
peningkatan ketajaman seperti halnya high pass filter ini digunakan untuk
memperbaiki hasil klasifikasi multispektral melalui teknik pemfiltran
mayoritas. Piksel-piksel terasing dapat di hilangkan filter mayoritas dirancang
berdasarkan suatu asumsi bahwa fenomena geografis bersifat keruangan.
6.4.3 filter tekstur
Penggunaan
metode jendela bergerak juga dapat diterapkan untuk mengubah informasi pada
suatu citra sehingga menonjolkan kenampakan teksturnya . tekstur adalah
frekuensi perubahan rona dalam ruang pada tingkat resolusi terkecil yang dapat
di amati secara visual. Pada suatu area tertentu , suatu kenampakan dapat
dikatakan bertekstur halus kalau laju perubahan rrona yang ada relatif kecil.
Sebaliknya tekstur dikatakan kasar apabila laju perubahan rona dalam ruang
observasi juga besar serta bersifat tidak gradual.
Apabila cara
berpikir diterpakan pada citra
pengindraan jauh maka bisa dikatakan bahwa semakin homogen nilai pikselnya,
atau semakin halus pula teksturnya. Begitu pula sebaliknya. Penilaina
kuantitatif tekstur dengan demikian dapat dilakukan dengan memperhatikan
piksel-piksel yang bertetangga pada suatu ukuran area observasi tertentu.
Mekanisme
jendela bergerak pada filter tekstur pada dasarnya sama dengan filter-filter
lain. Perbedaanya terletak pada cara komputasi piksel-piksel yang berdampingan
dalam jendela tersebut. Mengingat bahwa kenampakan tekstural berkaitan dengan
frekuensi perubahan rona-rona piksel-piksel tersebut dan frekuensi perubahan
rona juga pada dasarnya terkait dengan beberapa parameter statistik seperti misalnya
simpangan baku,variansi dan julat minimum –maksimum maka setiap kelompok piksel
pada ukuran jendela tertentu dapat dihitung parameternya statistiknya dan nilai
hasil hasil komputasi ini ditempatkan pada piksel pusat jendela.
Gambar 6.13 Metode pemfilteran tekstural (Sumber : Danoedoro , 2006)
Beberapa
perangkat lunak seperti ENVI dan ERDAS imagine menggunakan simpangan
baku,rerata, variasi, julat minimum-mkasimum dan juga entropi untuk menyatakan
ukuran teksturnya, pada umumnya semakin kecil nilai hasil komputasinya, semakin
halus pula teksturnya. Melalui proses pemfilteran sepaerti ini, kenampakan
wilayah urban akan cenderung menunjukan nilai tekstural yang lebih tinggi
dibandingkan dengan wilayah rural. Khususnya apabila citra beresolusi spasial
sekitar 20-50 meter digunakan untuk analisis.
6.4.4 Agregasi tekstural
Cara komputasi
statistik untuk menonjolkan aspek tekstural tertentu dapat diadopsi melalui
proses agregasi, yang memberikan efek penurunan resolusi spasial. Danoedoro
(2005) menerapkan agregasi tekstural citra pankromatik quickbird dan landsat
ETM+, yang masing-masing bresolusi spasial 0,6m dan 15m menjadi citra baru
beresolusi 2,4m dan 3m yang pada dasarnya setara dengan citra multispektral untuk
sensor yang sama. Prinsip agregasi ini adalah mengelompokan piksel-piksel
resolusi spasial tinggi kedalam satu piksel beresolusi spasial
Gambar 6.14
Metode agregasi tekstural yang memberikan efek penurunan resolusi spasial
(Danoedoro, 2006)
Dengan
cara ini, setiap 4x4 piksel resolusi 0,6m dijadikan satu piksel baru beresolusi
2,4m, di mana nilai barunya bias diperoleh dari perhitungan rerata, simpangan
baku, ataupun variasi dari kelompok piksel penyusunannya. Begitu pula halnya dengan
setiap 2x2 piksel citra pankromatik langsat ETM+ yang diturunkan resolusinya
menjadi 30m, dengan nilai piksel baru yang merepresentasikan parameter
statistic tertentu. Informasi tekstural semacam ini dapat dimanfaatkan untuk
mengintegrasikan data pankromatik berusolusi spasial tinggi dengan data
multispectral sensor yang sama dalam suatu klasifikasi multispectral sensor
yang sama dalam suatu klasifikasi multispectral.
6.5 APLIKASI TEKNIK PEMFILTERAN DALAM STUDI
PENGINDRAAN JAUH
Apabila utama teknik pemfilteran
dalam pengindraan jauh ialah untuk pengenalan pola(pattern recognition), khususnya pola spasial objek. Banyak
penelitian menggunakan teknik – teknik pemfilteran untuk menonjolkan jenis
–jenis batuan atau litologi tertentu. Melalui teknik pemfilteran, variasi
relief yang kurang jelas pada citra asli dapat ditonjolkan sehingga topografi
suatu bentuklahan tertentu dapat dibedakan dari yang lain secara lebih baik.
Penggunaan teknik shadow filter dapat
menonjolkan perbedaan topografi perbukitan karst dari perbukitan batu pasir
terkikis sedang karena efek simulasi bayangan yang ditimbulkan mampu
menonjolkan perbedaan bentuk kubah dan igir yang cenderung membulat.
Penggunaan filter Laplace mampu menonjolkan kenampakan
kekar (joint) pada batuan dan juga
kelurusan (lineament) sehingga sangat
membantu dalam proses identifikasi batuan untuk pemetaan geologi atau
heomorfologi. Filter serupa juga dapat diterapkan untuk studi kekotaan dengan
menggunakan citra resolusi tinngi, misalnya SPO-5 pankromatik ataupun Quickbird
(0,6m – 2,4m), sehingga jaringan jalan dapat diperjelas; begitu pula blok –
blok bangunan yang bentuk, ukuran, pola, dan situasinya dapat membantu dalam
pengenalan kelas – kelas pemukiman kota.
Perpanduan teknik
pemfilteran,penajaman kontras dan penyusunan komposit yang tepat akan sangat
membantu dalam memperbaiki kualitas citra
yang akan diinterprestasi secara visual. Bila citra komposit hasil
perpaduan saluran – saluran asli yang telah difilter hendak digunakan sebagai
media pengambilan sampel, meksipun saluran – saluran asli tetap dipakai sebagai
masukan, diperlukan kehati – hatian dalam menilai variabilitas spectral objek
yang hendak diambil sebagai sampel. hal ini mudah dimengerti ,mengingat
kenampakan objek pada citra komposit tadi merupakan hasil perpaduan saluran
asli yang telah diubah variabilitas spektralnya.
Gambar 6.15 Perbandingan
hasil pemfilteran. Atas: citra asli Langsat TM 5, bawah: dengan penghalusan (smoothing).
Gambar 6.16 Perbandingan hasil pemfilteran untuk daerah
muara k
Gambar 6.17 Citra
elevasi yang terbentuk melalui pembuatan model elevasi digital wilayah Gunung
kidul, Daerah Istimewa Yogyakarta. Citra ini merupakan hasil interpolasi
kontur, dimana setiap nilai piksel menunjukkan elevasi dalam meter dan tersaji
pada resolusi spasial 30 meter.
Penggunaan citra yang telah terfilter, khususnya filter – filter high-pass atau penajaman tepi-sebagian dasar pengambilan titik-titik control untuk koreksi geometri juga perlu dipertimbangkan secara teliti. Filter – filter tersebut di atas cenderung memanipulasi nilai piksel untuk menonjolkan kesan visual yang lebih baik. Ada kalanya terjadi pergeseran posisi batas objek sebagai konsekuensi perubahan nilai; misalnya pada penerapan filter Laplace. Pergeseran sejauh satu hingga dua piksel ini, bagaimana pun juga, berpengaruh terhadap akurasi posisi titik – titik control, yang sebenarnya berupa piksel – piksel dengan koordinat tertentu.
Gambar 6.18 Gambar
atas dan bawah berturut – turut menunjukkan hasil pemfilteran citra pada Gambar
6.17 ke arah sumbu x (atas) dan sumbu y (bawah), di mana nilai piksel pada
masing – masing citra itu menunjukkan nilai beda tinggi piksel tetangganya
Gambar 6.19
Hasil pemfilteran shadow atau shaded
relief atas citra DEM pada Gambar 6.17. perhatikan bedanya pada kesan
relief dan arah bayangan, jika dibadingkan dengan pemfilteran arah x dan y pada
Gambar 6.18
Banyak penelitian mencoba
menggabungkan saluran – saluran spectral yang telah difilter tekstur sebagai
tambahan terhadap data saluran asli, untuk meningkatkan akurasi hasil
klasifikasi multispectral. Penelitian Danoedoro (2003), Chen ea al (2004) dan puissant et al (2005), misalnya, menunjukkan
bahwa filter tekstur pada ukuran jendela 7x7 mampu meningkatkan akurasi hasil
klasifikasi, khusunya ketika pembedaan kategori
penutupan dan penggunaan lahan tidak terlalu diperhatikan dan atau
proses klasifikasi mencoba menggunakan metode penanaman sampel – sampel
spectral sebagai objek penggunaan lahan secara langsung.
Penelitian Danoedoro dan Phinn
(2005) selanjutnya menunjukkan bahwa penggunaan filter tekstur untuk saluran –
saluran asli justu dapat menurunkan tingkat akurasi hasil klasifikasi, ketika
acuan yang digunakan berupa skema klasifikasi penutup lahan yang lebih
berorientasi pada kelas – kelas spectral (bukan kategori – kategori spasial.
Penelitian ini menunjukkan bahwa skema klasifikasi berperan sangat penting
dalam metode dan proses penurunan informasi.
DAFTAR PUSTAKA
Danoedoro.P. 2012 Pengantar
Penginderaan Jauh Digital. Yogyakarta: Andi